그리디 알고리즘 개념

그리디 알고리즘(탐욕법)은 현재 상황에서 지금 당장 좋은 것만 고르는 방법을 의미한다. 일반적인 그리디 알고리즘은 문제를 풀기 위한 최소한의 아이디어를 떠올릴 수 있는 능력을 요구합니다.

작동 방식

그리디 알고리즘은 다음과 같은 단계로 동작합니다.

문제를 하위 문제로 나눕니다.
각 하위 문제에 대해 가장 좋아 보이는 선택을 합니다.
선택한 해를 부분해 집합에 추가합니다.
부분해 집합이 최종 해답이 되는지 확인합니다.
만약 최종 해답이 아니라면, 2단계로 돌아가 반복합니다.

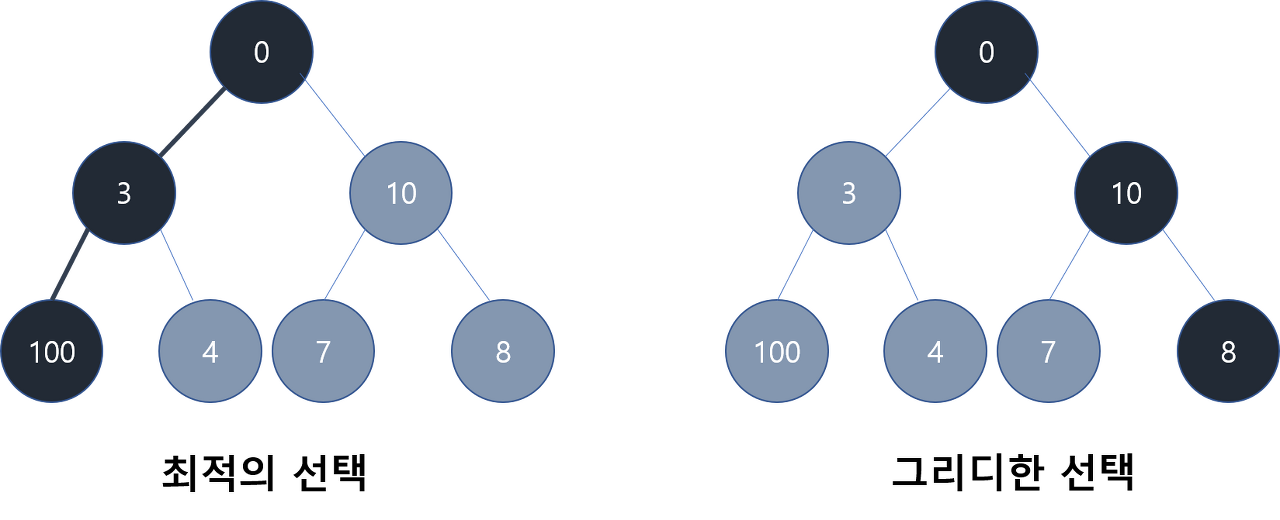
장단점

그리디 알고리즘의 주요 장점은 다음과 같습니다.

구현이 비교적 간단하다.
실행 속도가 빠르다.

하지만 그리디 알고리즘은 항상 최적해를 구할 수 있는 것은 아닙니다. 최적해를 보장하기 위해서는 추가적인 검증 단계가 필요할 수 있습니다. 그리디 알고리즘은 각 단계에서의 선택이 최적일 뿐, 그 선택들이 전체적으로 최적인지 보장하지 않기 때문입니다. 따라서 그리디 알고리즘을 사용할 때에는 문제의 성질과 제약 조건을 분석하여 최적해를 보장할 수 있는지 판단해야 합니다.

예시

문제: 거스름돈 문제

당신은 음식점의 계산을 도와주는 점원이다. 카운터에는 거스름돈으로 사용할 500원, 100원, 50원, 10원짜리의 동전이 무한히 존재한다고 가정한다. 손님에게 거슬러줘야 할 돈이 N원일 때 거슬러 줘야 할 동전의 최소 개수를 구하라. 단, 거슬러 줘야 할 돈 N은 항상 10의 배수이다.

해결 방법:

동전의 최소 개수를 구해야 하는 문제이기 때문에, 가장 큰 화폐 단위부터 돈을 거슬러 주는 것입니다.

거스름 돈이 N원일 때, 500원으로 최대한 많이 거슬러주고, 순서대로 100원, 50원, 10원을 써서 거슬러주면 됩니다.

이제 N이 1,260 일 때의 예시를 확인해봅시다.

코드

#include <stdio.h>

void giveChange(int amount) {
    int coins[] = {500, 100, 50, 10};  // 동전 종류
    int numCoins = sizeof(coins) / sizeof(coins[0]);  // 동전 종류의 개수
    int count[numCoins];  // 동전 개수를 저장할 배열

    // 각 동전의 개수 초기화
    for (int i = 0; i < numCoins; i++) {
        count[i] = 0;
    }

    // 가장 큰 동전부터 시작하여 거스름돈 주기
    for (int i = 0; i < numCoins; i++) {
        while (amount >= coins[i]) {
            amount -= coins[i];
            count[i]++;
        }
    }

    // 거스름돈 출력
    for (int i = 0; i < numCoins; i++) {
        if (count[i] > 0) {
            printf("%d원 동전: %d개\n", coins[i], count[i]);
        }
    }
}

int main() {
    int amount = 1260;  // 거스름돈 금액
    giveChange(amount);
    return 0;
}

정당성 분석

가장 큰 화폐 단위부터 돈을 거슬러 주는 것이 최적의 해를 보장하는 이유는 무엇일까요?

가지고 있는 동전 중에서 큰 단위가 항상 작은 단위의 배수이므로 작은 단위의 동전들을 종합해 다른 해가 나올 수 없기 때문

Q) 만약에 800원을 거슬러 주어야 하는데 화폐 단위가 500원, 400원, 100원이라면 어떻게 될까요?

4개의 동전 / 2개의 동전

대부분의 그리디 알고리즘 문제에서는 이처럼 문제 풀이를 위한 최소한의 아이디어를 떠올리고 이것이 정당한지 검토할 수있어야 답을 도출할 수 있다.